Fungsi Naik dan Fungsi Turun

 

Tentunya kalian masih ingat dengan topik sebelumnya tentang menentukan titik maksimum, titik minimum, dan titik belok. Pada topik ini, kalian akan belajar tentang penggunaan turunan dalam menentukan nilai maksimum dan nilai minimum.

Definisi 1 :

Jika diberikan fungsi f dengan daerah asal Df dan x = c merupakan anggota Df, maka berlaku hubungan sebagai berkut :

1. f(c) adalah nilai maksimum fungsi f pada Df jika f(c) ≥ f(x) untuk semua x di Df
2. f(c) adalah nilai minimum fungsi f pada Df jika f(c) ≤ f(x) untuk semua x di Df
3. f(c) adalah nilai ekstrim fungsi f pada Df jika f(c) adalah nilai maksimum atau minimum fungsi f di Df

Definisi 2 :

Jika diberikan fungsi f dengan daerah asal Df dan interval (a,b) merupakan himpunan bagian dari Df, maka berlaku hubungan sebagai berkut :

1. f(c) adalah nilai maksimum lokal fungsi f pada interval (a,b) yang memuat c jika f(c)adalah nilai maksimum fungsi f pada (a,b)
2. f(c) adalah nilai minimum lokal fungsi f pada interval (a,b) yang memuat c jika f(c)adalah nilai minimum fungsi f pada (a,b)
3. f(c) adalah nilai ekstrim lokal fungsi f jika f(c) adalah nilai maksimum lokal atau nilai minimum lokal fungsi f[/important

Lalu, kapan terjadi nilai ekstrim lokal?

Kalian dapat menggunakan uji turunan pertama untuk menentukan nilai ekstrim lokal.

Jika fungsi f kontinu pada selang terbuka (a,b) yang memuat x = c, maka berlaku hubungan sebagai berikut :

1. Jika f'(x) > 0 untuk semua nilai x dalam selang (a,c) dan f'(x) < 0 untuk semua nilai x dalam selang (c,b), maka f(c) merupakan nilai maksimum lokal f
2. Jika f'(x) < 0 untuk semua nilai x dalam selang (a,c) dan f'(x) > 0 untuk semua nilai x dalam selang (c,b), maka f(c) merupakan nilai minimum lokal f
3. Jika f'(x) pada selang (a,c) dan (c,b), maka f(c) bukan merupakan nilai ekstrim lokal f

Agar lebih jelas, mari perhatikan gambar di bawah ini.

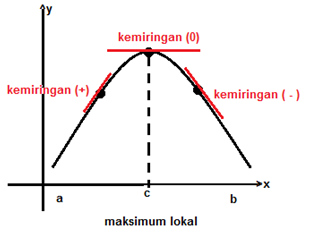
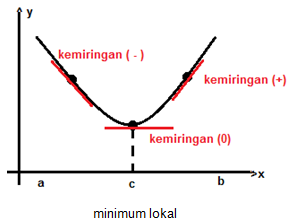
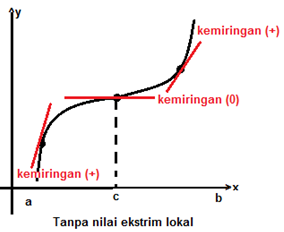
Apakah kalian sudah paham? Mari kita cermati beberapa contoh berikut ini.

Contoh 1:

Tentukan nilai maksimum dan minimum dari f(x) = 2x2 - x jika Df = { x | -1 ≤ x ≤ 2} !

Penyelesaian :

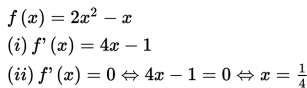
Jika kita perhatikan, ternyata x = ¼ merupakan anggota Df = { x | -1 ≤ x ≤ 2 }. Dengan demikian, untuk menentukan nilai maksimum dan nilai minimum fungsi f pada Df, kita perlu mengetahui nilai f untuk x = -1 , x = ¼, dan x = 2.

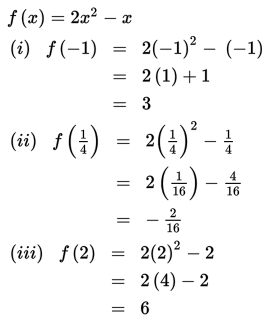
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari 
f(x) = 2x2 – x dengan Df = { x | -1 ≤ x ≤ 2 } berturut-turut adalah f(2) = 6 dan f( ¼ ) = - 1/8.

Contoh 2 :

Tentukan nilai maksimum dan minimum dari f(x) = 3x2 - 2x + 1 jika Df = { x | 1 ≤ x ≤ 4 } !

Penyelesaian :

Oleh karena x = 1/3 bukan merupakan anggota Df = { x | 1 ≤ x ≤ 4 }, maka untuk menentukan nilai minimum dan nilai maksimum untuk fungsi f, kita cukup mengetahui nilai f untuk x = 1 dan x = 4.

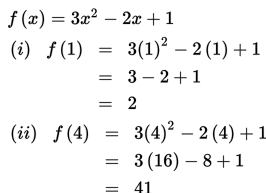
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari 
f(x) = 3x2 – 2x + 1 dengan Df = { x | 1 ≤ x ≤ 4 } berturut-turut adalah f(4) = 41 dan f(1) = 2.

Contoh 3 :

Tentukan nilai maksimum dan minimum dari f(x) = (x + 4)2 jika Df = { x | -4 ≤ x ≤ 0 } !

Penyelesaian :

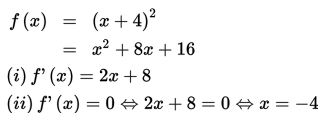
Oleh karena x = -4 merupakan batas kiri dari Df = { x | -4 ≤ x ≤ 0 }, maka untuk menentukan nilai minimum dan nilai maksimum untuk fungsi f, kita cukup mengetahui nilai f untuk x = -4 dan x = 0.

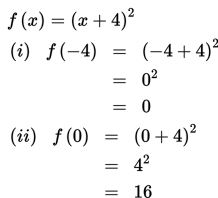
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari 
f(x) = (x + 4)2 dengan Df = { x | -4 ≤ x ≤ 0 } berturut-turut adalah f(0) = 16 dan f(-4) = 0.