MULIONO: Fungsi Komposisi

Fungsi komposisi merupakan suatu penggabungan dari operasi pada dua jenis fungsi f (x) dan g (x) sampai bisa menghasilkan fungsi baru.

Operasi fungsi komposisi juga biasa dinotasikan dengan penggunaan huruf atau simbol “o” yang dibaca sebagai komposisi atau bundaran.

Fungsi baru yang dapat terbentuk dari f (x) dan juga g (x), yakni:

(f o g)(x) = g dimasukkan ke f
(g o f)(x) = f dimasukkan ke g

Dalam fugsi komposisi juga dikenal dengan istilah fungsi tungal. Apa itu fungsi tunggal?

Fungsi tunggal sendiri adalah fungsi yang bisa dilambangkan dengan penggunaan huruf “f o g” maupun juga bisa dibaca sebagai“fungsi f bundaran g”.

Fungsi “f o g” ini merupakan suatu fungsi g yang dikerjakan terlebih dahulu kemudian dilanjutkan dengan f.

Sementara, untuk fungsi “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan suatu fungsi dengan f dikerjakan terlebih dahulu daripada g.

Fungsi Komposisi

Seperti yang tela disebutkan di atas, fungsi komposisi merupakan suatu penggabungan dari suatu operasi dua jenis fungsi f(x) dan juga g(x) sehingga mampu menghasilkan suatu fungsi baru.

Adapun rumus untuk fungsi komposisi, yaitu:

Rumus Fungsi Komposisi

Sperti yang terdapat pada uraian di atas, operasi untuk fungsi komposisi tersebut biasa dinotasikan dengan penggunakan huruf atau simbol “o”.

Di mana simbol tersebut bisa kita baca sebagai komposisi ataupun bundaran. Fungsi baru inilah yang bisa terbentuk dari f(x) dan g(x) yaitu:

1. (f o g)(x) yang berarti g dimasukkan ke f

2. (g o f)(x) yang berarti f dimasukkan ke g

Fungsi tunggal merupakan suatu fungsi yang dapat dinotasikan dengan penggunakan huruf “f o g” atau dapat dibaca “f bundaran g”.

Lalu Fungsi (f o g) (x) = f (g (x)) → fungsi g (x) dikomposisikan sebagai fungsi f (x)

Sementara itu, “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan fungsi f yang diselesaikan terlebih dahulu dari fungsi g.

Agar dapat memahami fungsi ini, perhatikan gambar dibawah ini :

fungsi komposisi f o g o h

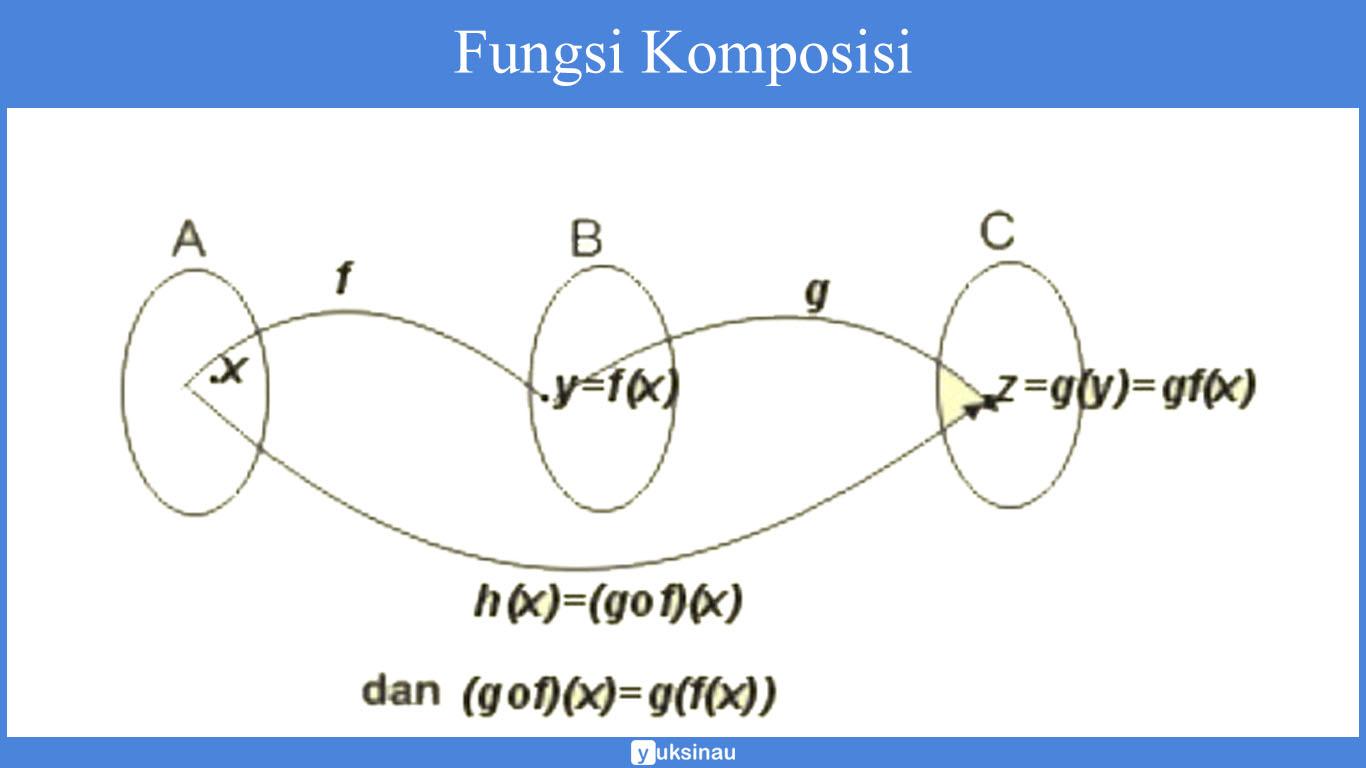
Dari skema rumus di atas, dapat kita ketahui bahawa:

Apabila f : A → B ditentukan dengan menggunakan rumus y = f(x)

Apabila g : B → C ditentukan dengan menggunakan rumus y = g(x)

Sehingga, akan kita peroleh hasil fungsi g dan f yaitu:

h(x) = (gof)(x) = g( f(x))

Dari definisi di atas maka bisa kita simpulkan jika fungsi yang melibatkan fungsi f dan g bisa kita tulis seperti berikut ini:

(g o f)(x) = g(f(x))
(f o g)(x) = f(g(x))

Sifat Sifat Fungsi Komposisi

Berikut akan kami berikan beberapa sifat dari fungsi komposisi, diantaranya adalah sebagai berikut:

Apabila f : A → B , g : B → C , h : C → D, maka akan berlaku beberapa sifat seperti:

(f o g)(x)≠(g o f)(x). Tidak berlaku sifat komutatif.
[f o (g o h)(x)] = [(f o g ) o h (x)]. Akan bersifat asosiatif.
Apabila fungsi identitas I(x), maka akan berlaku (f o l)(x) = (l o f)(x) = f(x).

Contoh Soal Fungsi Komposisi

Untuk memahami uraian di atas, berikut akan kami berikan contoh soal untuk fungsi komposisi yang sederhana, perhatikan baik-baik ya.

Soal 1.

Jika diketahui f (x) = 3x + 4 dan g (x) = 3x berapa nilai dari (f o g) (2)?

Jawab:

(f o g) (x) = f (g (x))

= 3 (3x) + 4

= 9x + 4

(f o g) (2) = 9(2) + 4

= 22

Gimana? Mudah bukan?

Fungsi Komposisi pada Kehidupan

Berikut akan kami berikan contoh fungsi komposisi yang ada dalam kehidupan sehari-hari, diantaranya yaitu:

1. Pembuatan buku bisa diproses lewat 2 tahap, antara lain:

Tahap editorial akan yang nantinya akan dilanjutkan dengan tahap produksi.
Di dalam tahap editorial, naskah akan kemudian di edit serta di layout menjadi file yang siap untuk dicetak.
Berikutnya, file diolah dalam tahap produksi mencetaknya supaya menjadi sebuah buku.
Proses pembuatan buku ini menggunakan penerapan dari algoritma fungsi komposisi.

2. Untuk mendaur ulang logam yakni:

Pada mulanya pecahan logam campuran akan dijadikan menjadi serpihan kecil.
Kemudian Drum magnetic yang terdapat di dalam mesin penghancur menyisihkan logam magnetic yang memuat unsure bes.
Lalu sisa dari pecahan logam dikeruk dan kemudian dipisahkan. Sementara untuk serpihan besi dilebur menjadi baja baru. Proses pendauran ulang logam tersebut menerapkan fungsi komposisi.

Untuk lebih jelasnya silakan simak videeo berikut :