Fungsi Komposisi pada aljabar dan penerapannya

 

Fungsi & Komposisi

Aljabar Fungsi

1. Penjumlahan f dan g

(f + g) (x) = f(x) + g(x).

Contoh Soal:

Diketahui f(x) = x + 2 dan g(x) = x2 – 4. Tentukan (f + g)(x).

Jawab:

(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2

2. Pengurangan f dan g

(f – g)(x) = f(x) – g(x).

Contoh soal

Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).

Jawab:

(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1

3. Perkalian f dan g

(f . g)(x) = f(x) . g(x).

Contoh soal

Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).

Jawab:

(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x

4. Pembagian f dan g

Contoh soal

Diketahui f(x) = x2 – 4 dan g(x) = x + 2. Tentukan

Jawab:

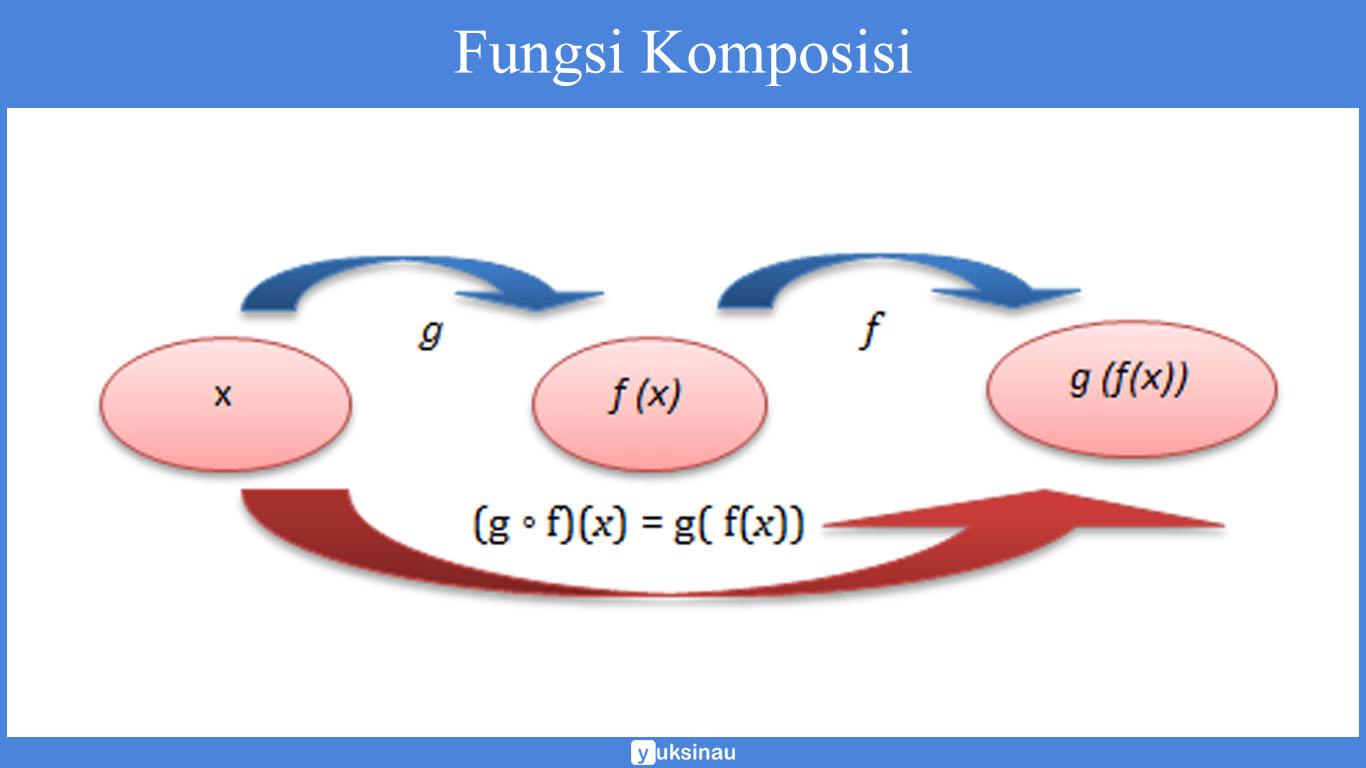
Fungsi Komposisi

Fungsi komposisi bisa kita tuliskan seperti berikut ini:

(f ◦ g)(x) = f (g (x))→ komposisi g (fungsi f bundaran g atau fungsi komposisi dengan g dikerjakan terlebih dahulu daripada f)

gambar 7

(g ◦ f)(x)= g (f (x))→ komposisi f (fungsi g bundaran f atau fungsi komposisi dengan f dikerjakan terlebih dahulu daripada g)

Sifat Fungsi Komposisi

1. Tidak berlaku sifat komutatif, (f ◦ g)(x) ≠ (g ◦ f)(x).
2. Berlaku sifat asosiatif, (f ◦(g ◦ h))(x) = ((f ◦ g)◦ h)(x).
3. Adanya unsur identitas (l)(x), (f ◦ l)(x) = (l ◦ f)(x) = f(x).

Contoh soal:

Diketahui f(x) = 2x – 1, g(x) = x2 + 2. Maka tentukan:

1. (g ◦ f)(x).
2. (f ◦ g)(x).
3. Apakah berlaku sifat komutatif: g ◦ f = f ◦ g?

Jawab:

1. (g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3

2. (f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3

3. Tidak berlaku sifat komutatif sebab g ◦ f ¹ f ◦ g.

Fungsi Invers

1. f-1 (x) adalah invers dari fungsi f(x)

2. Menentukan fungsi invers : mengganti f (x)= y = …” menjadi “ f -1 (y)= x = …”

3. hubungan sifat fungsi invers dengan fungsi komposisi:

1. (f ◦ f-1)(x)= (f -1 ◦ f)(x)= l (x)
2. (f ◦ g)-1 (x)= (g-1 ◦ f-1)(x)
3. (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g -1)(x)

Contoh Soal Fungsi Invers

Untuk memahami uraian di atas, berikut akan kami berikan contoh soal untuk fungsi komposisi yang sederhana, perhatikan baik-baik ya.

Soal 1.

Jika diketahui suatu fungsi f (x) = 5x +20, hitunglah fungsi invers f-1 (x)!

Jawab:

Jika fungsi f (x) dinyatakan dalam bentuk y sama dengan fungsi x → f (x) = y, maka:

f (x) = 5x + 20 → y = 5x + 20

Kemudian, merubah x menjadi f-1 (y), sehingga akan kita dapatkan:

y = 5x + 20

5x = y – 20

x = (y – 20)/5

x = y/5 – 4

f-1 (y) = y/5 – 4

f-1 (x) = x/5 – 4 → sehingga kita dapatkan fungsi invers dari f (x) = 5x + 20

Fungsi Invers dalam Kehidupan

Berikut akan kami berikan contoh fungsi invers yang ada dalam kehidupan sehari-hari, diantaranya yaitu:

1. Dalam Bidang Ilmu fungsi komposisi & inver di terapkan seperti:

• Pada Bidang Ekonomi
  Fungsi invers dipakai dalam menghitung sekaligus memperkirakan sesuatu, sebagai contoh fungsi permintaan dan penawaran.
• Pada Bidang Kimia
  Fungsi ivers digunakan dalam menentukan waktu peluruhan dari suatu unsur.
• Pada Bidang Geografi dan Sosiologi
  Fungsi invers dipagai dalam optimasi dalam industry  dan juga kepadatan penduduk.
• Pada Ilmu Fisika
  Fungsi invers dipakai untuk persamaan fungsi kuadrat dalam menjelaskan suatu fenomena gerak.

Contoh Soal dan Pembahasan

Setelah kalian memahami dengan baik mengenai fungsi komposisi, yuk coba kita kerjakan contoh soal di bawah ini:

Soal Fungsi Komposisi

Soal 1.

Diberikan dua buah fungsi di mana pada masing-masing f (x) dan g (x) berturut-turut yakni:

f (x) = 3x + 2
g (x) = 2 − x

Maka, tentukan:

a. (f o g) (x)
b. (g o f) (x)

Jawab:

Diketahui:

f (x) = 3x + 2
g (x) = 2 − x

a. (f o g)(x)

“Masukkan g (x) nya ke f (x)”

Sehingga akan kita dapatkan:

(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3 (2 − x) + 2
= 6 − 3x + 2
= − 3x + 8

b. (g o f ) (x)

“Masukkan f (x) nya ke g (x)”

Sehingga akan kita peroleh:

(f o g) (x) = g (f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x

Soal 2.

Diketahui suatu fungsi f (x) = 3x − 1 dan juga g (x) = 2×2 + 3. Nilai dari komposisi fungsi ( g o f )(1) yaitu?

A. 12
B. 8
C. 7
D. 11
E. 9

Jawaban

Diketahui:

• f (x) = 3x − 1 dan g (x) = 2×2 + 3

Ditanyakan:

( g o f )(1) =…?

Penyelesaian:

Masukkan f (x) nya ke dalam g (x), kemudian isi dengan 1, sehingga menjadi:

(g o f) (x) = 2 (3 x − 1) 2 + 3
(g o f) (x) = 2 (9 x 2 − 6x + 1) + 3
(g o f) (x) = 18x 2 − 12x + 2 + 3
(g o f) (x) = 18×2 − 12x + 5
(g o f) (1) = 18 (1) 2 − 12(1) + 5 = 11

Jawabannya : D

Soal 3.

Diketehui dua buah fungsi, yaitu sebagai berikut:

f (x) = 2x − 3
g (x) = x2 + 2x + 3

Apabila (f o g)(a) merupakan 33, maka tentukanlah nilai dari 5a!

Jawab:

Langkah pertama adalah mencari terlebih dahulu (f o g)(x), yaitu:

(f o g)(x) sama dengan 2(x2 + 2x + 3) − 3
(f o g)(x) sama dengan 2×2 4x + 6 − 3
(f o g)(x) sama dengan 2×2 4x + 3

33 sama dengan 2a2 4a + 3
2a2 4a − 30 sama dengan 0
a2 + 2a − 15 sama dengan 0

Lalu faktorkan hingga menjadi:

(a + 5)(a − 3) sama dengan 0
a = − 5 maupun a sama dengan 3

sampai kita peroleh:

5a = 5(−5) = −25 atau 5a = 5(3) = 15

Soal 4.

Apabila (f o g)(x) = x² + 3x + 4 serta g(x) = 4x – 5. Tentukan nilai dari f(3)!

Jawab:

(f o g)(x) sama dengan x² + 3x + 4

f (g(x)) sama dengan x² + 3x + 4

g(x) sama dengan 3 Jadi,

4x – 5 sama dengan 3

4x sama dengan 8

x sama dengan 2

f (g(x)) = x² + 3x + 4 serta untuk g(x) sama dengan 3 diperoleh x sama dengan 2

Sehingga kita ketahui: f (3) = 2² + 3 . 2 + 4 = 4 + 6 + 4 = 14

Soal 5. (UN Matematika SMA IPA – 2010 P04)

Diketahui fungsi f(x) = 3x − 1 dan g(x) = 2x2 + 3. Nilai dari komposisi fungsi (g o f)(1) =….

A. 7
B. 9
C. 11
D. 14
E. 17

Jawab:

Diketahui:

• f(x) = 3x − 1 dan g(x) = 2x2 + 3

Ditanyakan:

• (g o f)(1) =…….

Masukkan f(x) nya pada g(x) lalu isi dengan angka 1, sehingga akan menjadi:

(g o f)(x) = 2(3x − 1)2 + 3
(g o f)(x) = 2(9x2 − 6x + 1) + 3
(g o f)(x) = 18x2 − 12x + 2 + 3
(g o f)(x) = 18x2 − 12x + 5
(g o f)(1) = 18(1)2 − 12(1) + 5 = 11

Jawaban: C

Soal 6. (SIMAK UI 2013 DASAR)

Diketahui suatu f -1 (4x-5) = 3x-1 dan (f -1 ◦ f)(5)= p2 +2p – 10 maka rata-rata dari nilai p adalah…

a. -4
b. -2
c. -1
d. 1
e. 4

Jawab:

f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1

Sehingga akan kita peroleh 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2

Menentukan nilai p

(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3

Sehingga, rata-rata nilai p adalah (-5) + 3 / 2 = -1

Jawaban: C

Soal Fungsi Invers

Soal 1.

Tentukan rumus fungsi invers dari fungsi f(x) = 2x + 6.

Jawab:

Soal 2.

Tentukan rumus fungsi invers dari fungsi gambar di bawah ini:

Soal 3. (SIMAK UI 2013 DASAR)

Diketahui f -1 (4x-5) = 3x-1 dan (f -1 ◦ f)(5)= p2 +2p – 10 maka rata-rata dari nilai p adalah…

1. -4
2. -2
3. -1
4. 1
5. 4

Jawab:

f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2

Menentukan nilai p

(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3

Sehingga, rata-rata nilai p yaitu 

Jawabannya adalah C

Soal 4.  (UN 2004)

Sebuah pemetaan f:R→R dengan (g ◦ f)(x) = 2x2 + 4 x + 5 dan g(x) = 2x + 3. Maka f(x)=…

1. x2 + 2x + 1
2. x2 + 2x + 2
3. 2x2 + x + 2
4. 2x2 + 4x + 2
5. 2x2 + 4x + 1

Jawab:

Menentukan f(x)

(g ◦ f)(x) = 2x2 + 4x + 5
g(f(x)) = 2x2 + 4x + 5
2(f(x)) + 3 = 2x2 + 4x + 5
f(x) = x2 + 2x + 1

Jawabannya: A

Soal 5. (SNMPTN 2010 Dasar)

Jika g(x – 2) = 2x – 3 dan (f ◦ g)(x – 2) = 4x2 – 8x + 3, maka f(-3) =…

1. -3
2. 0
3. 3
4. 12
5. 15

Jawab:

g(x – 2) = 2x – 3
(f ◦ g)(x – 2) = 4x2 – 8x + 3
f(g(x – 2)) = 4x2 – 8x + 3
f(2x – 3) = 4x2 – 8x + 3

Menentukan f(-3)
Jika -3 = 2x – 3 maka x = 0
Sehingga:
f(-3) = 4(0)2 – 8(0) + 3 = 3

Jawabannya: A

Soal 6. (SIMAK UI 2012 DASAR)

Misalkan f : R→ R dan g : R→R, f(x) = x + 2 dan (g ◦ f)(x) = 2x2 + 4x – 6, Misalkan juga x1dan x2 adalah akar-akar dari g(x) = 0 maka x1 + 2x2 =…

1. 0
2. 1
3. 3
4. 4
5. 5

Jawab:

Menentukan g(x).

(g ◦ f)(x) = 2x2 + 4x – 6
g(f(x)) = 2x2 + 4x – 6
g(x+2) = 2x2 + 4x -6
g(x) = 2(x – 2)2 + 4(x – 2) – 6 = 2x2 – 8x + 8 + 4x – 8 – 6 = 2x2 – 4x – 6

Menentukan x1 + 2x2

g(x) = 0
2x2 – 4x – 6 = 0
x2 – 2x – 3 = 0
(x-3)(x+1) = 0
x1=3 →x2 = -1, jadi 3
x1 = 2x2 = 3+2 (-1) = 1

atau

x1 = -1 → x2 = 3, jadi
x1 + 2x2 = (-1) + 2(3) = 5

Jawabannya: E