Pengertian Kesebangunan

foto berskala merupakan salah satu contoh penerapan konsep kesebangunan dalam kehidupan sehari-hari. Apa pengertian kesebangunan?

Untuk lebih mudah memahami apa pengetian dari kesebangunan silahkan perhatikan gambar persegi panjang ABCD dan PQRS di bawah ini! 

 

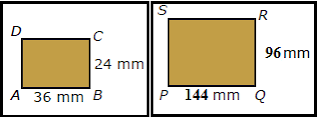Pada persegi panjang ABCD memiliki panjang dan lebar yaitu 36 mm dan 24 mm, serta persegi panjang PQRS memiliki panjang dan lebar yaitu 58 mm dan 38 mm.

Perbandingan antara panjang persegipanjang ABCD dan panjang persegi panjang PQRS adalah 36 : 144 atau 1 : 4. Demikian pula dengan lebarnya, perbandingannya 24 : 96 atau 1 : 4. Dengan demikian, sisi-sisi yang bersesuaian dari kedua persegipanjang itu memiliki perbandingan senilai (sebanding). Perbandingan sisi yang bersesuaian dari kedua persegipanjang tersebut, yaitu sebagai berikut.

AB/PQ = BC/QR = CD/RS = AD/PS = ¼

Oleh karena semua sudut persegipanjang besarnya 90° (siku-siku) maka sudut-sudut yang bersesuaian dari kedua persegipanjang itu besarnya sama. Dalam hal ini, persegipanjang ABCD dan persegipanjang PQRS memiliki sisi-sisi bersesuaian yang sebanding dan sudut-sudut bersesuaian yang sama besar. Selanjutnya, kedua persegipanjang tersebut dikatakan sebangun. Jadi, persegipanjang ABCD sebangun dengan persegipanjang PQRS.

Pengertian kesebangunan seperti ini berlaku umum untuk setiap bangun datar. Dua bangun datar dikatakan sebangun jika memenuhi dua syarat berikut:

1. Panjang sisi-sisi yang bersesuaian dari kedua bangun itu memiliki perbandingan senilai.
2. Sudut-sudut yang bersesuaian dari kedua bangun itu sama besar.

Untuk memantapkan pemahaman Anda tentang pengertian kesebangunan, silahkan perhatikan contoh soal di bawah ini.

Contoh Soal 1

Jika persegipanjang ABCD sebangun dengan persegi panjang PQRS, hitung panjang QR.

Penyelesaian:

Salah satu syarat dua bangun dikatakan sebangun adalah sisi-sisi yang bersesuaian sebanding. Oleh karena itu,

AB/PQ = BC/QR

2/6 = 5/QR

2QR = 30

QR = 15

Jadi, panjang QR adalah 15 cm.

Contoh Soal 2

Jika layang-layang KLMN dan layang-layang PQRS pada gambar di bawah ini sebangun, tentukan besar ∠R dan ∠S.

Penyelesaian:

Salah satu syarat dua bangun dikatakan sebangun adalah sudut-sudut yang bersesuaian sama besar sehingga ∠P = 125° dan ∠Q = 80°. Amati layang-layang PQRS, menurut sifat layang-layang, sepasang sudut yang berhadapan sama besar sehingga ∠R = ∠P = 125°. Oleh karena sudut dalam layang-layang berjumlah 360° maka

<=> ∠P + ∠Q + ∠R + ∠S = 360°
<=> ∠S = 360° – (∠P + ∠Q + ∠R)
<=> ∠S = 360° – (125° + 80° + 125°)

<=> ∠S = 360° – 330° 
<=> ∠S = 30°