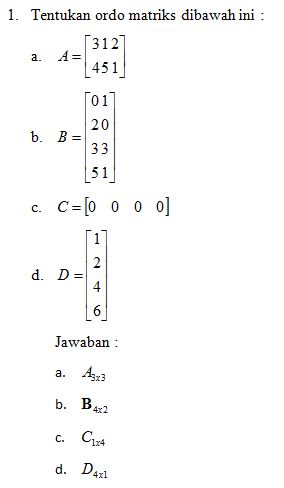E. Operasi Aljabar pada Matriks
a. Penjumlahan Matriks
Jika A dan B dua buah matriks berordo sama maka jumlah matriks A dan B ditulis A+B adalah sebuah matriks baru C yang diperoleh dengan menjumlahkan elemen-elemen matriks A dengan elemen-elemen B yang seletak.
Contoh 12
Pada penjumlahan belaku sifat- sifat :1. Komutatif, A+B = B+A2. Asosiatif, ( A+B)+C = A+(B+C)3. Sifat lawan, A+(-A) = 04. Identitas penjumlahan, A+0 = A
b. Pengurangan Matriks
Pengurangan matriks A dengan matriks B adalah suatu matriks yang elemen-elemenya diperoleh dengan cara mengurangkan elemen matriks A dengan elemen matriks B yang besesuaian (seetak), atau dapat pula diartikan sebagai menjumlahkan matriks A dengan lawan negative dari B, dituliskan: A-B = A+(-B).
Seperti halnya pada penjumlahan dua buah matriks, pengurangan dua buah matriks pun terdefinisi apabila ordo kedua matriks tersebut sama.
c. Soal-Soal dan penyelesaian Matriks.
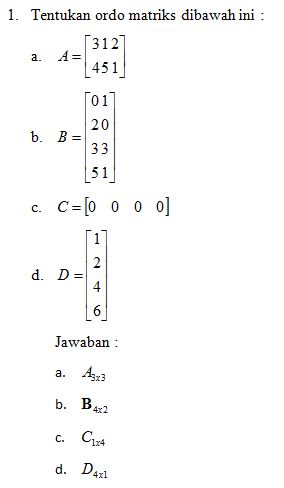

Jika A dan B dua buah matriks berordo sama maka jumlah matriks A dan B ditulis A+B adalah sebuah matriks baru C yang diperoleh dengan menjumlahkan elemen-elemen matriks A dengan elemen-elemen B yang seletak.
Contoh 12

Pada penjumlahan belaku sifat- sifat :
1. Komutatif, A+B = B+A
2. Asosiatif, ( A+B)+C = A+(B+C)
3. Sifat lawan, A+(-A) = 0
4. Identitas penjumlahan, A+0 = A
b. Pengurangan Matriks
Pengurangan matriks A dengan matriks B adalah suatu matriks yang elemen-elemenya diperoleh dengan cara mengurangkan elemen matriks A dengan elemen matriks B yang besesuaian (seetak), atau dapat pula diartikan sebagai menjumlahkan matriks A dengan lawan negative dari B, dituliskan: A-B = A+(-B).
Seperti halnya pada penjumlahan dua buah matriks, pengurangan dua buah matriks pun terdefinisi apabila ordo kedua matriks tersebut sama.
c. Soal-Soal dan penyelesaian Matriks.