Penerapan Listrik Statis

 

Analisis listrik statis

Hukum Coulomb

 Gambar 11. Interaksi dua benda bermuatan

(sumber: physics principle and problems)

Dua benda bermuatan saling didekatkan seperti gambar di atas, akan saling berinteraksi. Gambar 11(a) menunjukkan interaksi antara dua benda bermuatan positif akan saling menjauhi (tolak menolak), begitu pula jika dua benda yang sama-sama bermuatan negatif (gambar 11b) jika didekatkan akan saling menjauhi (tolak-menolak), akan tetapi benda bermuatan negatif didekatkan ke benda bermuatan positif (gambar 11c) maka akan  saling mendekat (tarik-menarik).

Gaya interaksi antara dua benda bermuatan (atau dua muatan) disebut dengan gaya listrik atau gaya Coulomb sesuai dengan nama penemunya. Gaya listrik ini pertama kali diteliti oleh ilmuan yang bernama Charles Augustin de Coulomb (1736-1806) berdasarkan eksperimennya mengemukakan hukum coulomb yakni “besarnya gaya listrik antara dua muatan sebanding dengan besar muatan dan berbanding terbalik dengan kuadrat jaraknya” secara matematis dapat dituliskan

Keterangan :

F_C : gaya coulomb (N)

k : tetapan (9 x 10⁹ Nm²/C²)

q₁ & q₂ : besar muatan (C)

r : jarak kedua muatan (m)

Jurus jitu:

Dalam banyak kasus atau soal terkait dengan materi gaya Coulomb, sering kali kita dihadapkan pada masalah perbandingan antara gaya listrik dengan besar muatan, gaya listrik dengan kuadrat jarak antar muatan atau bahkan keduanya. Untuk menyelesaikan permasalahan ini hal penting yang perlu dipahami adalah

·      Besar gaya Coulomb sebanding dengan besar muatan

Konsep sebanding:

“Perhatikan letak indeks (a dan b)masing-masing variabel yang sama antara ruas kiri dan ruas kanan”

·      Besar gaya Coulomb berbanding terbalik dengan kuadrat jarak

Konsep berbanding terbalik

 “Perhatikan letak indeks (a dan b)masing-masing variabel yang berlawanan antara ruas kiri dan ruas kanan”

Indeks “a” untuk keadaan awal dan indeks “b” untuk keadaan akhir.

Sehingga persamaan perbandingan untuk hukum Coulomb adalah

Contoh soal:
Gambar berikut menunjukkan gaya tolak-menolak antara dua benda titik bermuatan listrik

Besar gaya tolak menolak antara kedua benda tersebut jika muatan listrik diganti menjadi +2Q dan +Q, dan jarak kedua benda menjadi 2d adalah…

a.  ½ F                         b.   2F                          c.   4F                          d.   8F

Pembahasan:

Keadaan awal

q_1a = +Q

q_2a = +Q

r_a = d

F_a = F

Keadaan akhir

q_1b = +2Q

q_2b = +Q

r_b = 2d

F_b = ..... ?

Soal merupakan perbandingan antara gaya listrik, muatan pertama dan jarak. Persamaan perbandingannya adalah.

Kunci jawaban : “D”

perlu diingat bahwa gaya termasuk besaran vektor sehingga selain besarnya gaya juga harus diperhatikan arahnya juga seperti gambar berikut.

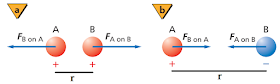
 Gambar 12. (a) gaya interaksi dua muatan berbeda jenis, (b) gaya interaksi dua muatan sejenis

(sumber: physics principle and problems)

Dua muatan sejenis yang didekatkan akan saling menjauhi dengan arah gaya seperti yang ditunjukkan oleh gambar 12a, sedangkan dua muatan yang berbeda jenis didekatkan akan saling  mendekati seperti yang ditunjukkan oleh gambar 12b. Berdasarkan gambar terlihat baik muatan A dan muatan B keduanya saling memberikan gaya kepada kedua muatan (F_B on A maupun F_A on B), kedua gaya ini adalah pasangan gaya aksi dan reaksi (hukum III Newton)

Salah satu penerapan dari hukum Coulomb ini adalah pada penggunaan elektroskop. Elektroskop merupakan alat yang digunakan untuk mendeteksi suatu benda bermuatan atau tidak

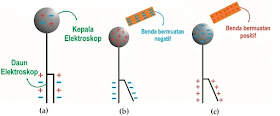
Prinsip kerja dari elektroskop dapat dilihat dari gambar berikut:

 Gambar 13. Prinsip kerja elektroskop

Pada mula-mula elektroskop bermuatan netral sehingga muatan positif (proton) dan negatif (elektron) tersebar merata di seluruh elektroskop (gambar 12a) dan daun elektroskop dalam keadaan tertutup, kemudian benda bermuatan listrik negatif di dekatkan (tanpa bersentuhan) ke kepala elektroskop (gambar 12b), muatan negatif benda tersebut akan membuat muatan positif elektroskop tertarik ke kepala elektroskop dan muatan negatifnya tertolak hingga menuju daun elektroskop. Kedua bilah daun elektroskop akan bermuatan negatif, hal ini akan menimbulkan gaya interaksi (gaya listrik) saling tolak menolak sehingga membuat daun elektroskop terbuka (gambar 12c)

Medan Listrik

Seperti yang sudah dijelaskan sebelumnya bahwa dua muatan yang didekatkan akan saling berinteraksi satu Medan listrik merupakan daerah di sekitar muatan yang masih dipengaruhi oleh gaya listrik (gaya coulomb). Medan listrik pada sebuah muatan digambarkan oleh garis-garis gaya listrik dengan Arah medan listrik adalah keluar dari muatan positif dan masuk ke dalam muatan negatif, seperti yang ditunjukkan oleh gambar berikut.

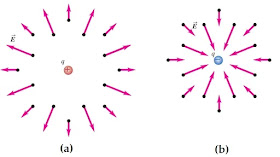
 Gambar 14. Arah medan magnet (a) muatan positif, (b) muatan negatif

(sumber: physics university)

Besarnya medan listrik pada suatu titik yang berjarak r dari sebuah muatan dapat ditentukan dengan persamaan matematis.

Keterangan :

E : medan listrik (N/C)

q : muatan listrik (C)

r : jarak (m)

k : tetapan (9 x 10⁹ Nm²/C²)

gambar medan magnet untuk dua muatan yang saling berinteraksi dapat digambarkan sebagai berikut.

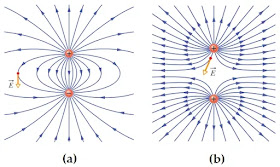
Gambar 15. Arah medan magnet dua muatan yang berinteraksi (a) muatan positif dan negatif, (b) muatan positif dan positif.

(sumber : fundamentals of physics)

Sumber :

Glencoe.Electricity and magnetism. Mc Graw Hill. 2005

Glencoe. Physics Principle and Problems. Mc Graw Hill. 2005

Resnick, R., Halliday, D., Walker, J. Fundamentals of Physics, 10^th ed., John Wiley & Sons, Inc. 2014

Young, H. D., Freedman, R. A. Sears ana Zemansky’s university physics : with modern physics 13^th ed., Pearson education, Inc.2012

Untuk lebih jelasnya silakan simak Video berikut : 

Perkalian Bilangan Bulat

 Perkalian Bilangan Bulat

Kita ketahui bahwa perkalian merupakan operasi penjumlahan berulang dengan bilangan yang sama. Agar lebih memahami maksud pernyataan tersebut silahkan perhatikan contoh berikut.

3 × 2 = 2 + 2 + 2 = 6

2 × 3 = 3 + 3 = 6

Meskipun hasil akhirnya sama, perkalian 3 × 2 dan 2 × 3 memiliki arti yang berbeda, di mana 3 × 2 artinya tiga kali duanya, sedangkan 2 × 3 artinya dua kali tiganya. Secara umum, pernyataan tersebut dapat dituliskan bahwa “Jika n adalah sebarang bilangan bulat positif maka: n × a = a + a + a . . . + a, di mana n merupakan banyaknya suku a”

Penerapan dalam kehidupan sehari-hari tentang konsep perkalian yakni pada saat kita berobat ke klinik, puskesmas atau rumah sakit. Misalnya dokter menulis 3 x 1 pada kotak sirup, itu artinya supaya pasien meminum sirup tersebut satu sendok takar sesuai anjuran dokter dalam sehari sebanyak tiga kali (pagi, siang, dan malam sesudah makan). Akan berbeda maksudnya jika ditulis 1 x 3, itu berati pasien meminum obat tersebut tiga sendok takar sesuai anjuran dokter dalam sehari hanya sekali (bisa pagi, siang atau malam).

Perkalian Bilangan Bulat Positif dan Negatif

Untuk mengetahui operasi perkalian bilangan bulat positif dan negatif, silahkan perhatikanlah contoh-contoh berikut.

a. 2 × (–6) = –12

b. 3 × (–6) = –18

c. 4 × (–6) = –24

d. 5 × (–6) = –30

e. 6 × (–6) = –36

Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa hasil kali bilangan bulat positif dengan bilangan bulat negatif adalah bilangan bulat negatif. Di mana Untuk setiap bilangan bulat a dan b selalu berlaku a × (– b) = – (a × b).

Perkalian Dua Bilangan Bulat Negatif

Untuk mengetahui operasi perkalian dua bilangan bulat negatif, silahkan perhatikanlah contoh-contoh berikut.

a. 2 × (–6) = –12

b. 1 × (–6) = –6

c. 0 × (–6) = 0

d. –1 × (–6) = 6

e. –2 × (–6) = 12

Berdasarkan contoh soal d dan e di atas, maka dapat disimpulkan bahwa hasil kali dua bilangan bulat negatif adalah bilangan bulat positif. Di mana untuk setiap bilangan bulat a dan b selalu berlaku (– a) × (– b) = (a × b).

Perkalian Bilangan Bulat dengan Nol (0)

Untuk mengetahui operasi perkalian bilangan bulat positif dengan nol (0), silahkan perhatikanlah contoh-contoh berikut.

a. 6 × 0 = 0

b. –6 × 0 = 0

c. 0 × 6 = 0

Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa untuk semua bilangan apabila dikalikan dengan nol (0) hasilnya adalah nol.

Unsur Identitas pada Perkalian

Sekarang perhatikan contoh soal di bawah ini.

a. 10 × 1 = 10

b. 5 × 1 = 5

c. –5 × 1 = –5

d. –3 × 1 = –3

Berdasarkan contoh soal di atas maka dapat ditarik kesimpulan bahwa semua bilangan bulat bila dikalikan dengan 1, akan menghasilkan bilangan itu sendiri. Dalam hal ini 1 disebut unsur identitas pada perkalian. Jadi, untuk setiap bilangan bulat a selalu berlaku a × 1 = 1 × a = a.

Oke

Pengurangan Bilangan Bulat

Untuk menjumlahkan bilangan bulat dapat dilakukan dengan alat bantu yakni dengan garis bilangan. Bagaimana dengan pengurangan pada bilangan bulat? Sama seperti pada penjumlahan pada bilangan bulat, pengurangan pada bilangan bulat juga bisa menggunakan alat bantu berupa garis bilangan. Oke sekarang silahkan simak penjelasaannya di bawah ini.

Kita ketahui bahwa pengurangan dinyatakan sebagai penjumlahan dengan lawan bilangan pengurang. Konsep ini sudah Anda pelajari pada waktu Anda duduk di bangku sekolah dasar. Coba ingat-ingat kembali konsep tersebut.

Oke untuk mengingat kembali konsep tersebut, silahkan bandingkan hasil penjumlahan 4 + (–3) dan pengurangan 4 – 3. Dengan menggunakan bantuan garis bilangan maka untuk menjumlahkan 4 + (–3) dapat dilakukan dengan langkah-langkahnya berikut ini.

=> Gambarlah anak panah dari angka 0 sejauh 4 satuan ke kanan sampai pada angka 4.

=> Gambarlah anak panah tadi dari angka 4 sejauh 3 satuan ke kiri sampai angka 1

=> Jadi, hasilnya dari 4 + (–3) = 1 dan garis bilangannya akan tampak seperti gambar di bawah ini.

Sedangkan untuk pengurangan 4 – 3 sama seperti langkah-langkahnya di atas yakni.

=> Gambarlah anak panah dari angka 0 sejauh 4 satuan ke kanan sampai pada angka 4.

=> Gambarlah anak panah tadi dari angka 4 sejauh 3 satuan ke kiri sampai angka 1.

=> Jadi, hasilnya dari 4 + (–3) = 1 dan garis bilangannya akan tampak seperti gambar di bawah ini.

Sekarang kita bandingkan hasil penjumlahan –5 + 2 dengan pengurangan –5 – (–2). Dengan cara yang sama seperti cara di atas maka hasil penjumlahan –5 + 2 maka garis bilangannya akan tampak seperti gambar di bawah ini.

Sedangkan hasil pengurangan –5 – (–2), gambar garis bilangannya akan tampak seperti gambar di bawah ini.

Setelah melihat kedua hasil pengurangan dan penjumlahan di atas dengan bantuan garis bilangan maka diperoleh bahwa:

=> 4 – 3 = 4 + (–3) = 1

=> –5 – (–2) = –5 + 2 = –3

Jadi, berdasarkan pemaparan di atas, maka dapat disimpulkan bahwa pada pengurangan bilangan bulat, mengurangi dengan suatu bilangan sama artinya dengan menambah dengan lawan pengurangnya. Secara umum pernyataan tersebut dapat dituliskan bahwa “untuk setiap bilangan bulat a dan b, maka berlaku a – b = a + (–b)”.

Oke